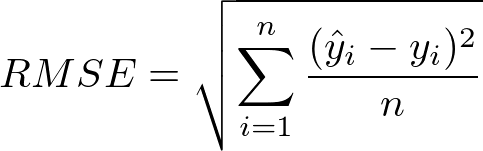Disini kita akan bahas salah satu model statistik yang umum digunakan untuk Machine Learning untuk melakukan prediksi dengan cara supervised learning, yaitu regresi linear. Metode ini melibatkan 2 variabel dimana salah satunya adalah variabel independen (x) dan satu lagi adalah variabel dependen (y).
- Independen berarti variabel ini sebagai variabel utama yang mungkin akan mempengaruhi nilai variabel kedua (dependen).
- Dependen berarti nilai variabel ini akan tergantung dari nilai variabel independennya, jika korelasi tinggi maka dependensi juga tinggi.
Untuk memudahkan pemahaman, kita gunakan data sample berat dan tinggi badan dari 10 orang sebagai berikut ini:
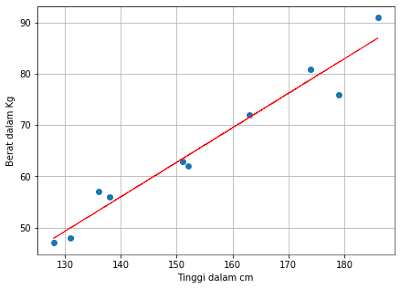
Data Tinggi Badan(cm) : 151,174,138,186,128,136,179,163,152,131 Data Berat Badan (Kg) : 63, 81, 56, 91, 47, 57, 76, 72, 62, 48
Regresi Linear adalah proses mencari garis linear yang menujukkan korelasi antara kedua variabel tersebut, garis linear itu akan didapat dengan sebuah persamaan :
y = ax + b atau y = w1x + w0 dimana: a atau w1 adalah slope / gradient / coefficient b atau w0 adalah intercept / bias
Ciri dari problem regresi ini adalah kasusnya diminta menebak angka. Jenis outputnya bersifat continuous. Contoh lain dari regresi ini misalnya menebak curah hujan, harga rumah, jumlah kendaraan pemudik, dsb.
Perhitungan Manual
Untuk mendapatkan nilai coef(A) dan intercept/bias(B) digunakan rumus:
Gambar diatas menjelaskan detail perhitungan dari rumus tersebut kedalam excel. Dalam mencari nilai coef A dan intercept/bias B di excel digunakan formula pada sheet berikut:
A =((C25*C24)-(C23*C21))/((C25*C22)-(C23*C23)) B =((C21*C22)-(C23*C24))/((C25*C22)-(C23*C23))
Menggunakan Python
Perhitungan di python lebih sederhana, dimana kita bisa menggunakan library sklearn, seperti pada contoh kode dibawah ini:
Nilai coef dan intercept didapatkan dari kode baris ke-19 dan-20 diatas, sehingga akan didapatkan persamaan linear sebagai berikut:
y = 0.674 * x + (-38.455)
Sedangkan hasil dari plot data seperti pada gambar dibawah, dimana garis merah merupakan nilai prediksi dari model linear regresi dan titik-titik biru adalah 10 data training yang digunakan.
Regresi Linear Berganda
Regresi Linear Berganda adalah model regresi linear dengan melibatkan lebih dari satu variable bebas/independen dan persamaannya adalah
y = a1x1 + a2x2 + .. + anxn + b
Untuk pembahasan prediksi menggunakan regresi liner berganda kali ini akan diambil dari paper yang telah dipublish oleh mas Ervan Triyanto di jurnal Rabit, Juli 2019. Kasus ini adalah prediksi jumlah produksi padi di kabupaten Bantul dengan data yang digunakan dari tahun 2009 sampai dengan 2017. Di penelitian tersebut perhitungan nya diimplementasikan ke dalam aplikasi web menggunana PHP sebagai bahasa pemrogramannya. Di artikel ini akan digunakan python untuk perhitungannya dengan alasan kemudahannya.
Downlod pada link ini untuk mendapatkan artikelnya.
Terdapat 1 variabel dependen yaitu jumlah produksi padi (dalam ton), sedangkan terdapat 3 variabel independen yaitu: curah hujan, luas lahan dan tingkat serangan hama.
Berikut contoh code di Python untuk menghitung kasus produksi padi diatas:
Dari data diatas, didapatkan persamaan untuk prediksi sebagai berikut:
y = 5.929528x1 + 118.27991767x2 -175.71483753x3 + 8306.792151921123 dimana: luas lahan(x1), curah hujan(x2) dan hama(x3)
Evaluasi
Evaluasi untuk model linear regresi dapat dilakukan dengan beberapa metrik evaluasi seperti: MAE (Mean Absolute Error), MSE (Mean Squared Error) atau RMSE (Root Mean Squared Erorr).
RMSE merupakan salah satu cara untuk mengevaluasi model regresi linear dengan mengukur tingkat akurasi hasil perkiraan suatu model. RMSE dihitung dengan mengkuadratkan error (prediksi – observasi) dibagi dengan jumlah data (rata-rata), lalu diakarkan. RMSE tidak memiliki persamaan:
Pada kode python diatas, evaluasi model dituliskan pada baris kode ke-50 dengan menggunakan library metrics dari sklearn dan didapatkan score RMSE yaitu: 3.5045
Kesimpulan
Jika membutuhkan dataset tersebut bisa tulis email pada komentar ya.. Bisa anda gunakan untuk penelitian dengan metode machine learning lainya dan silahkan dibandingkan nilai errornya dengan penelitian ini.
Referensi
- Jimy, Regresi Linier dengan R dan Python, https://medium.com/@jrendz/regresi-linier-dengan-r-dan-python-ebb80662c6da
- Jasme Moody,What does RMSE really mean?, https://towardsdatascience.com/what-does-rmse-really-mean-806b65f2e48e
- Triyanto, E., Sismoro, H., & Laksito, A. (2019). Implementasi Algoritma Regresi Linear Berganda untuk Memprediksi Produksi Padi di Kabupaten Bantul. Rabit : Jurnal Teknologi Dan Sistem Informasi Univrab, 4(2), 73-86. https://doi.org/10.36341/rabit.v4i2.666